g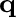 ν( ν( , i, j) = , i, j) =    〈ψi, 〈ψi, | |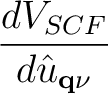 ⋅ ⋅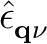 | ψj, | ψj, + +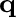 〉. 〉.
|
(1) |
The electron-phonon coefficients g are defined as
g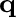 ν( ν( , i, j) = , i, j) =    〈ψi, 〈ψi, | |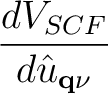 ⋅ ⋅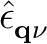 | ψj, | ψj, + +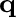 〉. 〉.
|
(1) |
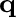 ν is defined by
ν is defined by
γ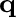 ν = 2πω ν = 2πω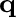 ν ν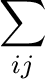 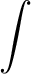 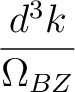 | g | g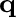 ν( ν( , i, j)|2δ(e , i, j)|2δ(e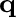 , i - eF)δ(e , i - eF)δ(e + +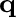 , j - eF), , j - eF),
|
(2) |
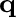 ν for
mode ν at wavevector
ν for
mode ν at wavevector 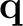 is defined as
is defined as
λ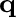 ν = ν = 
|
(3) |
α2F(ω) = 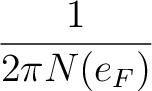 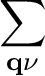 δ(ω - ω δ(ω - ω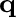 ν) ν)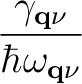 . .
|
(4) |
λ = 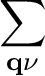 λ λ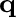 ν = 2 ν = 2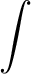 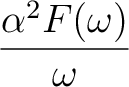 dω. dω.
|
(5) |
Note that a factor M-1/2 is hidden in the definition of normal modes as used in the code.
McMillan:
Tc = 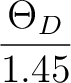 exp exp 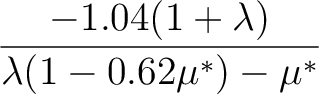 ![$\displaystyle \left.\vphantom{
{-1.04(1+\lambda)\over \lambda(1-0.62\mu^*)-\mu^*}}\right]$](img25.png)
|
(6) |
Tc =  exp exp 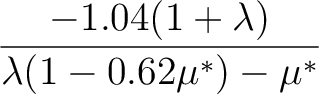 ![$\displaystyle \left.\vphantom{
{-1.04(1+\lambda)\over \lambda(1-0.62\mu^*)-\mu^*}}\right]$](img25.png)
|
(7) |
ωlog = exp 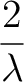 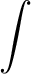  α2F(ω)logω α2F(ω)logω![$\displaystyle \left.\vphantom{ {2\over\lambda} \int {d\omega\over\omega}
\alpha^2F(\omega) \mbox{log}\omega }\right]$](img30.png)
|
(8) |