


Next: 4.4 DFPT with the
Up: 4 Using PHonon
Previous: 4.2 Calculation of interatomic
Contents
Since v.5.0, there are two ways of calculating electron-phonon
coefficients, distinguished according to the value of variable
electron_phonon. The following holds for the case
electron_phonon= 'interpolated' (see also Example 03).
The calculation of electron-phonon coefficients in metals is made difficult
by the slow convergence of the sum at the Fermi energy. It is convenient to
use a coarse k-point grid to calculate phonons on a suitable
wavevector grid;
a dense k-point grid to calculate the sum at the Fermi energy.
The calculation
proceeds in this way:
- a scf calculation for the dense
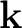 -point grid (or a scf calculation
followed by a non-scf one on the dense
-point grid (or a scf calculation
followed by a non-scf one on the dense 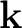 -point grid); specify
option la2f=.true. to pw.x in order to save a file with
the eigenvalues on the dense k-point grid. The latter MUST contain
all
-point grid); specify
option la2f=.true. to pw.x in order to save a file with
the eigenvalues on the dense k-point grid. The latter MUST contain
all 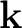 and
and
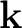 +
+ 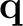 grid points used in the subsequent
electron-phonon
calculation. All grids MUST be unshifted, i.e. include
grid points used in the subsequent
electron-phonon
calculation. All grids MUST be unshifted, i.e. include 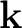 = 0.
= 0.
- a normal scf + phonon dispersion calculation on the coarse k-point
grid, specifying option electron_phonon='interpolated', and
the file name where
the self-consistent first-order variation of the potential is to be
stored: variable fildvscf).
The electron-phonon coefficients are calculated using several
values of Gaussian broadening (see PHonon/PH/elphon.f90)
because this quickly
shows whether results are converged or not with respect to the
k-point grid and Gaussian broadening.
- Finally, you can use matdyn.x and lambda.x
(input documentation in the header of PHonon/PH/lambda.f90)
to get the
α2F(ω) function, the electron-phonon coefficient
λ, and an estimate of the critical temperature Tc.
See the appendix for the relevant formulae.
Important notice: the
q→ 0 limit of the contribution
to the electron-phonon coefficient diverges for optical modes! please
be very careful, consult the relevant literature.



Next: 4.4 DFPT with the
Up: 4 Using PHonon
Previous: 4.2 Calculation of interatomic
Contents
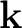 -point grid (or a scf calculation
followed by a non-scf one on the dense
-point grid (or a scf calculation
followed by a non-scf one on the dense 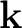 -point grid); specify
option la2f=.true. to pw.x in order to save a file with
the eigenvalues on the dense k-point grid. The latter MUST contain
all
-point grid); specify
option la2f=.true. to pw.x in order to save a file with
the eigenvalues on the dense k-point grid. The latter MUST contain
all 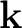 and
and
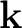 +
+ 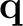 grid points used in the subsequent
electron-phonon
calculation. All grids MUST be unshifted, i.e. include
grid points used in the subsequent
electron-phonon
calculation. All grids MUST be unshifted, i.e. include 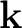 = 0.
= 0.